Markov Chain Monte Carlo (MCMC) is a computational technique used to approximate complex probability distributions. It works by constructing a Markov chain that has the desired distribution as its equilibrium distribution. By running this Markov chain for a sufficiently long time, samples drawn from it can be used to approximate the target distribution.

One of the algorithms that are used to implement a Markov Chain Monte Carlo is the Metropolis-Hastings algorithm. The Metropolis-Hastings algorithm is a Markov Chain Monte Carlo (MCMC) method used for sampling from a probability distribution, especially when direct sampling is difficult. Here’s a breakdown of the algorithm:

1. Initialization: Start with an initial state for the Markov chain.

2. Proposal: Propose a new state from a proposal distribution. This distribution suggests where to move next in the state space.

3. Acceptance/Rejection: Calculate an acceptance probability based on the ratio of the target distribution at the proposed state and the current state, adjusted by the proposal distribution. This ratio represents the likelihood of moving from the current state to the proposed state.

   1. If the proposed state has a higher probability according to the target distribution, accept it with probability 1.
   2. If the proposed state has a lower probability, accept it with probability equal to the ratio of probabilities.

4. Update: Move to the proposed state based on the acceptance probability. If rejected, stay in the current state.

5. Repeat: Repeat steps 2-4 for a predetermined number of iterations or until convergence is achieved.

The key idea behind Metropolis-Hastings is that even though it’s only a random walk in the state space, the ratio of the target distribution’s probabilities ensures that the samples generated will eventually converge to the desired distribution.

The Metropolis-Hastings algorithm ensures that the Markov chain generated converges to the desired distribution regardless of the choice of the proposal distribution, as long as it satisfies certain conditions.

Here’s a simple example of using MCMC, specifically the Metropolis-Hastings algorithm, to sample from a normal distribution:

import numpy as np
import matplotlib.pyplot as plt

# Target distribution (normal distribution)
def target_distribution(x, mu, sigma):
    return np.exp(-0.5 * ((x - mu) / sigma)**2) / (np.sqrt(2 * np.pi) * sigma)

# Proposal distribution (normal distribution for simplicity)
def proposal_distribution(x, sigma_proposal):
    return np.random.normal(x, sigma_proposal)

# Metropolis-Hastings algorithm
def metropolis_hastings(num_samples, mu, sigma, sigma_proposal, initial_state=0):
    samples = [initial_state]
    accepted = 0

    for _ in range(num_samples):
        current_state = samples[-1]
        proposed_state = proposal_distribution(current_state, sigma_proposal)

        # Calculate acceptance probability
        acceptance_prob = min(1, target_distribution(proposed_state, mu, sigma) /
                                      target_distribution(current_state, mu, sigma))

        # Accept or reject proposal
        if np.random.rand() < acceptance_prob:
            samples.append(proposed_state)
            accepted += 1
        else:
            samples.append(current_state)

    acceptance_rate = accepted / num_samples
    return samples, acceptance_rate

# Parameters
num_samples = 10000
mu = 0
sigma = 1
sigma_proposal = 1

# Run Metropolis-Hastings algorithm
samples, acceptance_rate = metropolis_hastings(num_samples, mu, sigma, sigma_proposal)

# Plot histogram of samples
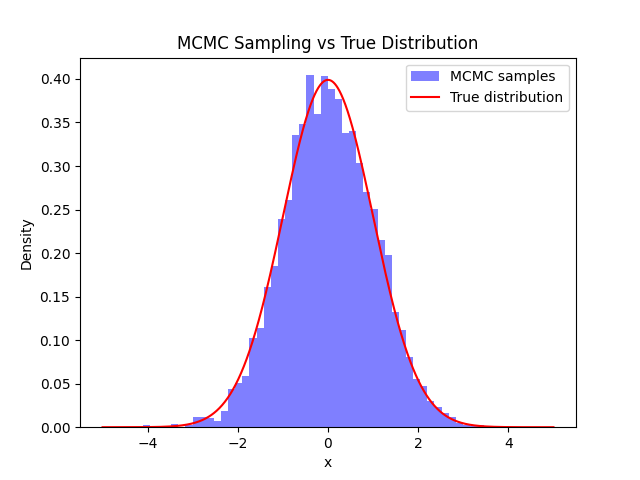
plt.hist(samples, bins=50, density=True, alpha=0.5, color='b', label='MCMC samples')
plt.plot(np.linspace(-5, 5, 1000), target_distribution(np.linspace(-5, 5, 1000), mu, sigma),
         color='r', label='True distribution')
plt.title('MCMC Sampling vs True Distribution')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.show()

print(f'Acceptance rate: {acceptance_rate}')

This code generates samples from a normal distribution using the Metropolis-Hastings algorithm and plots the resulting distribution along with the true distribution.