In mathematics a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.

The simplest example of a random walk is the random walk of the integer line, with starting point the number 0, and at each step moves +1 or -1 with equal probability.

The above example is an one-dimensional random walk and will be the first random walk that we will see in this post.

The theory

To define this walk formally, take independent random variables Ζ₀, Ζ₁, Ζ₂ .. where each variable is either 1 or −1, with a 50% probability for either value and set S₀ = 0 and S_n as the sum of all previous Ζ_i till Ζ_n.

The series {S_n} is called the simple random walk on the integer line.

The code.

To generate this simple random walk in python we will use the numpy library to generate the random numbers and the matplotlib library to visualize them. To begin, first we create a file named random_walk.py and import the necessary libraries.

import numpy as np
import matplotlib.pyplot as plt

Then we create an empty list named random_walk which we will use to store each of our data points and initialize it at 0.

random_walk = [0]

The next step is to choose the number of steps we want our walk to run for, in this example we choose 100, and generate that much random integers that are either 0 or 1 to simulate the 50% chance.

steps = 100
random_numbers = np.random.randint(0,2,steps)

Now we are ready to create our Random walk, we will loop through our random number list and we check if the number at each time step is either 1 or 0. If the number is 0 we will add 1 to our previous data point else if the number is 1 we will subtract 1 from our previous data point.

for r in random_numbers:
    if r == 0:
        step=1
    else:
        step=-1
    random_walk.append(random_walk[-1]+step)

After all that we can visualize the walk using the matplotlib library as follows.

plt.plot(random_walk)
plt.title("Simple Random Walk")
plt.xlabel("Time steps")
plt.ylabel("Current Position")
plt.show()

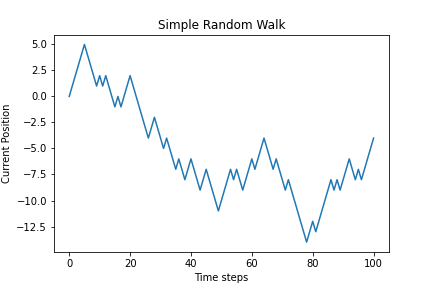
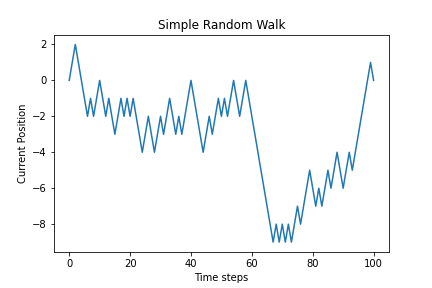
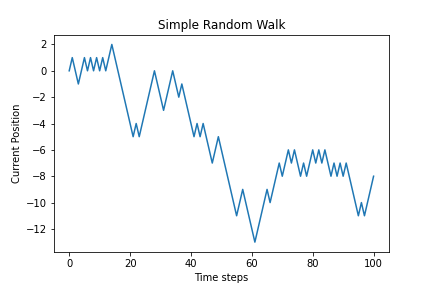
As we can see after running the code 3 times, we get different random walks that’s to be expected due the nature of the process.

The full code for this article can be found at github